Image Denoising with Markov Random Fields

20 Apr 2020

I found this problem as an assignment in WnCC IITB’s excellent initiative CodeInQuarantine, do give it a look.

progress

Denoising in Action

Algorithm

We’ll be using a quadratic MRF prior \(g\) to penalize the difference between neighbouring pixel intensities. \begin{align} g(u) = |u|^2 \end{align}

We will start from a blank image a update its values via gradient descent to minimize our objective \(f\). Here \(x_{i_1},x_{i_2},x_{i_3},x_{i_4}\) are surrounding pixels of \({x_i}\).

\begin{align} f(x, y) = \sum_{i} [ a(x_i-y_i)^2 + \sum_{n=1}^{4} g(x_i-x_{i_n})] \end{align}

Instead of calculating gradients manually, we take advantage of PyTorch’s autograd.

Implementation

The code for this project is available in this Colab Notebook and will soon be on GitHub.

The image to denoise is an MRI scan of a brain.

Noisy Image

Ground Truth

Let’s start writing code

import numpy as np
import torch
from matplotlib import pyplot as plt
from PIL import Image
from torchvision.transforms import ToTensor
from torch.optim import RMSprop

Define our objective function

def mrf_prior(x, a=0):
    return x**2

def mrf_loss(X, noisy, a):
    loss1 = ((noisy - X)**2).sum()
    loss2 = 0
    loss2 += mrf_prior(X[:, 1: ] - X[:, :-1]).sum()
    loss2 += mrf_prior(X[:-1, :] - X[ 1:, :]).sum()
    return a*loss1 + 2*loss2

We’ll start with a completely black image.

to_tensor = ToTensor()
RRMSE = lambda x: (((gt - x)**2).sum() / (gt**2).sum())**0.5
noisy = to_tensor(Image.open('mri_image_noise_level_high.png'))[0].cuda()
gt    = to_tensor(Image.open('mri_image_noiseless.png'))[0].cuda()
X = torch.zeros_like(noisy).cuda()
X.requires_grad = True
errors = []
losses = []
images = []
alpha  = 6.7
optimizer = RMSprop([X])
n_it   = 100

Writing the optimization loop.

for it in range(n_it):
    optimizer.zero_grad()
    loss = mrf_loss(X, noisy, alpha)
    loss.backward()
    optimizer.step()
    errors.append(RRMSE(X))
    losses.append(loss.item())
    images.append(np.array(255*X.clone().detach()).astype(np.uint8))

The last line just stores our image as a numpy array in a lost so we can convert it to a GIF using imageio library.

Result

We compare both images using Relative Root Mean Squared Error.

RRMSE Initial: 0.15553350746631622
RRMSE Final  : 0.1274341344833374

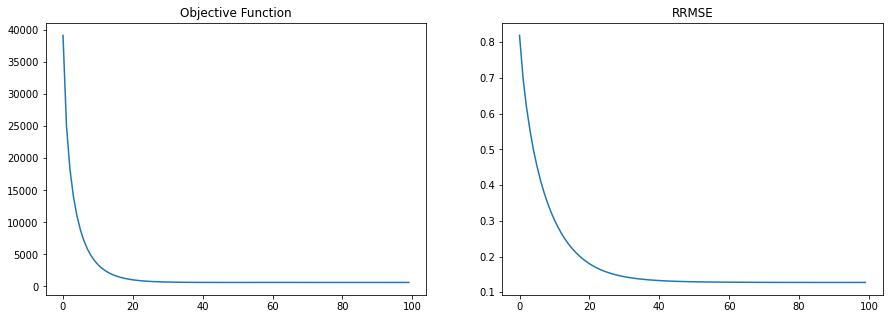
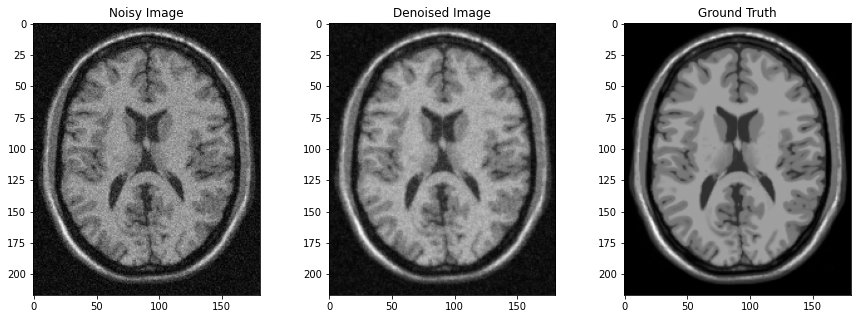
Denoising Results

Comments

Related Posts