Harris Corner Detection in Python

Algorithm

The algorithm can detect corners and edges effectively. It uses structural information from the structure tensor’s eigenvalues to find change in intensity values and their direction. A much detailed explanation can be found at Harris Corner Detection.

Implementation

I will be implementing the algorithm in Python using NumPy and I will use the following image to demonstrate.

Source Code

The full project code is available at GitHub.

Image Derivatives

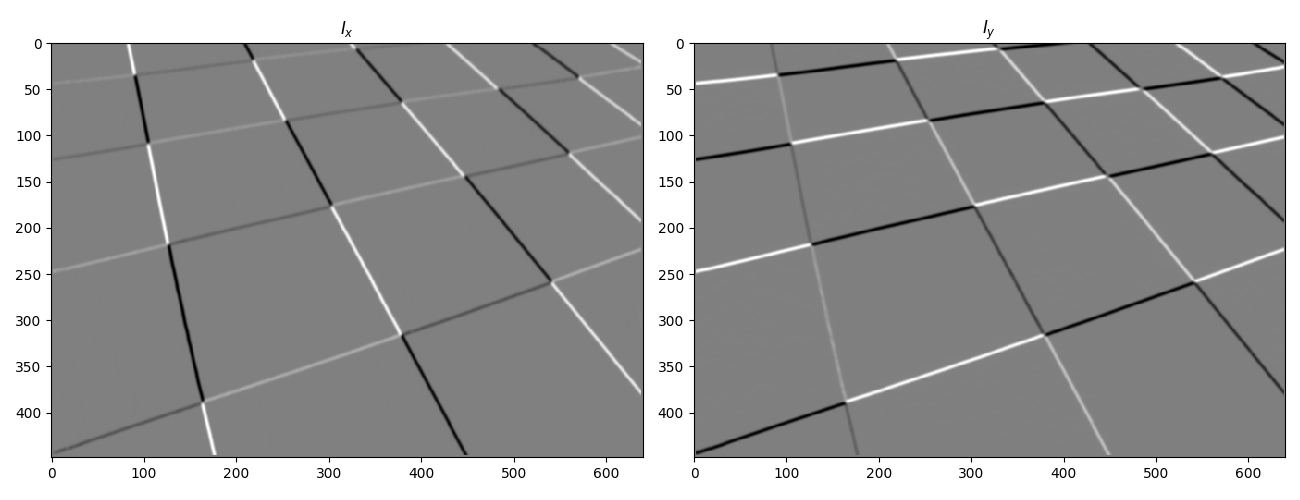
We’ve used Sobel operators of aperture 3 to compute \(I_x\) and \(I_y\) . Since the Sobel operators are seperable filters (have rank 1), we have used the optimised algorithm for calculating the derivatives. We define the following function to filter an image $I$ with a seperable filter whose factors are filter_y\(_{(1×3)}\) and filter_x\(_{(3×1)}\)

def seperable_conv(I, filter_x, filter_y):
    h, w = I.shape[:2]
    n = filter_x.shape[0]//2
    I_a = np.zeros(I.shape)
    I_b = np.zeros(I.shape)
    for x in range(n, w-n):
        patch = I[:, x-n:x+n+1]
        I_a[:, x] = np.sum(patch * filter_x, 1)
    filter_y = np.expand_dims(filter_y, 1)
    for y in range(n, h-n):
        patch = I_a[y-n:y+n+1, :]
        I_b[y, :] = np.sum(patch * filter_y, 0)
    return I_b

Now, for Sobel derivatives, we just take the filters as \([−1, 0, 1] , [1, 2, 1]^T\) and vice-versa.

def detect(I, n_g, n_w, k):
    h, w = I.shape
    sobel_1 = np.array([-1, 0, 1])
    sobel_2 = np.array([1, 2, 1])
    I_x = seperable_conv(I, sobel_1, sobel_2)
    I_y = seperable_conv(I, sobel_2, sobel_1)
    ...

We now apply gaussian blur to smoothen the image. Since gaussian filter is also seperable, we take advantage of this fact and use the above function.

def gaussian_mask(n, sigma=None):
    if sigma is None:
        sigma = 0.3 * (n // 2) + 0.8
    X = np.arange(-(n//2), n//2+1)
    kernel = np.exp(-(X**2)/(2*sigma**2))
    return kernel

def detect(I, n_g, n_w, k):
    ...
    g_kernel = gaussian_mask(n_g)
    I_x = seperable_conv(I_x, g_kernel, g_kernel)
    I_y = seperable_conv(I_y, g_kernel, g_kernel)
    D_temp = np.zeros((h,w,2,2))
    ...

Structure Tensor

\begin{align} \left.A = \sum_{u}\sum_{v}w(u,v)\begin{bmatrix} I_x^2 & I_xI_y \\I_xI_y & I_y^2\end{bmatrix} \right |_{u,v} \end{align}

Using the smoothened derivatives \(I_x, I_y\), we calculate the structure tensor \(A\) at every pixel.

def detect(I, n_g, n_w, k):
    ...
    D_temp = np.zeros((h,w,2,2))
    D_temp[:,:,0,0] = np.square(I_x)
    D_temp[:,:,0,1] = I_x*I_y
    D_temp[:,:,1,0] = D_temp[:,:,0,1]
    D_temp[:,:,1,1] = np.square(I_y)
    g_filter = gaussian_mask(n_w)
    g_filter = np.dstack([g_filter]*4).reshape(n_w, 2, 2)
    D = seperable_conv(D_temp, g_filter, g_filter)
    ...

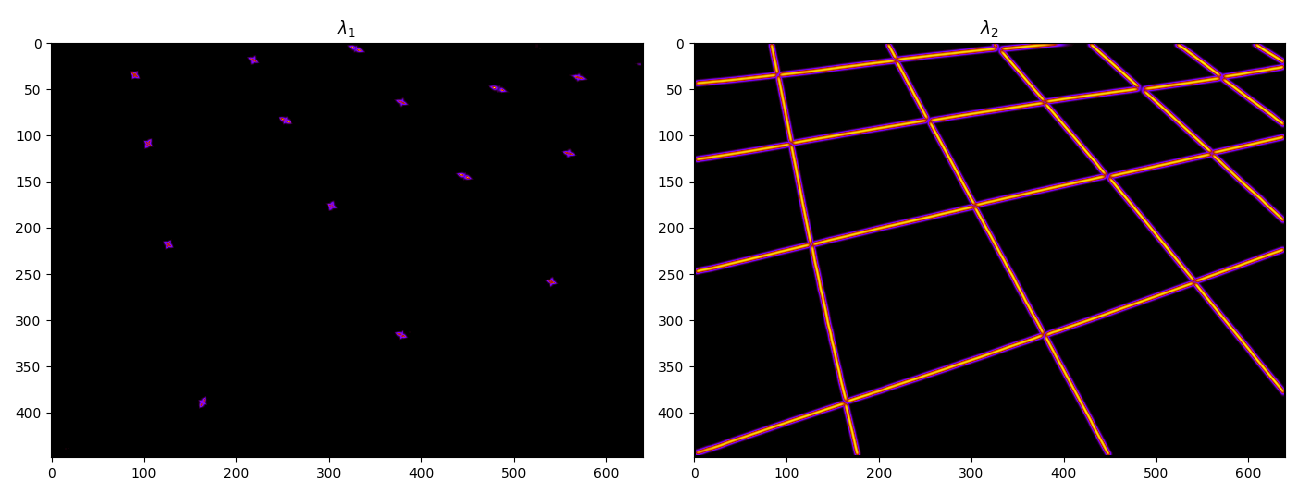
Eigenvalues

Since A is a \(2×2\) matrix. It’s eigenvalues have a closed form solution.
Let,

\begin{align} A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \end{align}

Then,

\begin{align} \lambda_{1,2} = \frac{a+d}{2}\pm\frac{\sqrt{(a-d)^2+4bc}}{2} \end{align}

def detect(I, n_g, n_w, k):
    ...
    P = D[:, :, 0, 0]
    Q = D[:, :, 0, 1]
    R = D[:, :, 1, 1]
    T1 = (P+R)/2
    T2 = np.sqrt(np.square(P-R)+4*np.square(Q))/2
    L_1 = T1-T2
    L_2 = T1+T2
    ...

Cornerness Measure

Cornerness measure \(C\) was calculated and thresholded at \(0.457\) (found emperically).

\begin{align} C = \lambda_1\lambda_2-k(\lambda_1+\lambda_2)^2 \end{align}